Fully nonlinear simulations of upstream waves at a topography

John Grue

Mechanics Division, Department of Mathematics, University of Oslo, Norway

Introduction

The aim of this paper is to describe recent research at the University of Oslo on internal waves generated upstream of a topography. Our investigations have both practical and general motivations. The practical needs relate to offshore activity in deep water and to certain proposed installations in coastal water like submerged floating tunnels. In both cases the effects due to internal waves may be important. It is of interest in this connection, among others, to investigate how internal waves in an actual ocean basin or fjord may be generated.
 

Two-layer model

Here we focus on waves in a two-layer fluid generated by flow over topography. We have developed a two-dimensional, transient, fully nonlinear model for this purpose. The two-fluid system has a lower layer with thickness h₁ and constant density $\rho_1$, and an upper layer with thickness h₂ and constant density $\rho_2<\rho_1$. A coordinate system O-xy is introduced with the x-axis along the interface at rest and the y-axis pointing upwards. We model the flow in each of the layers by potential theory. A Lagrangian method is adopted, where pseudo Lagrangian particles are introduced on the interface, each with a weighted velocity defined by $\mbox{\bf v}_{\times}=(1-\alpha)\mbox{\bf v}_{1}+\alpha\mbox{\bf v}_{2}$, where $\mbox{\bf v}_{1}$ and $\mbox{\bf v}_{2}$ denote the fluid velocities in the respective layers, and $0\le\alpha\le 1$. The prognostic equations are obtained from the kinematic and dynamic boundary conditions at the interface, i.e.

$$D_{\times}(x,y)/dt=\mbox{\bf v}_{\times},\hspace{0.5cm}D_{\time......box{\bf v}_{2})-(1/2)(\mbox{\bf v}_{1}^{2}-\mu\mbox{\bf v}_{2}^{2})-(1-\mu)gy$$

where $\mu=\rho_2/\rho_1$, $D_{\times}/dt=\partial/\partial t+\mbox{\bf v}_{\times}\cdot\nabla$ and the gravity g acts downwards. The prognostic equations are expanded in Taylor series, keeping several terms, in order to obtain an efficient scheme. Accurate solution of the Laplace equation is crucial to an algoritm for computing interfacial flows, and we here apply complex theory and Cauchy's integral theorem for this purpose.

For interfacial waves with finite amplitude the physical Kelvin-Helmholtz instability is inevitably included in the theoretical model. This represents a difficulty since the space discretization cannot be too fine. Instability is removed by a regridding procedure and smoothing. We are, however, able to document convergence of the method and accuracy in all cases considered. The mathematical model is documented in reference 1.
 

Undulating bore

In the first example we apply the model to fluid layers with thicknesses h₂ and h₁=4h₂, and densities $\rho_2=0.8$ g cm^-3 and $\rho_1=0.986$ g cm^-3. A body, starting from rest, is moving horizontally with speed U in the upper layer, and we shall compute the resulting motion of the interface. The shape of the body is determined by y=h₂-H₀sech²(Kx), where H₀=0.4h₂ and KH₀=0.1989. This configuration corresponds to a set of experiments described by Melville & Helfrich (1987). (We have been able to simulate their experiments with good agreement using the present fully nonlinear method, where weakly nonlinear KdV-theory exhibits severe shortcomings). First we consider two examples where the speed of the body is either U=0.81c₀ or U=0.94c₀, where c₀ in the linear shallow water speed of the two-fluid system. The resulting profiles of the interface exhibit an undular depression that is developing ahead of the body, with a number of oscillations which is increasing with time, see figure 1. Behind the body an almost horizontal elevation develops, with length which also is increasing with time. We find that the results in figure 1 are typical for speed of the body in the interval 0.38< U/c₀<1.02, approximately, for this configuration. The lower limit corresponds to the lower limit of the transcritical regime.
 

Solitary waves

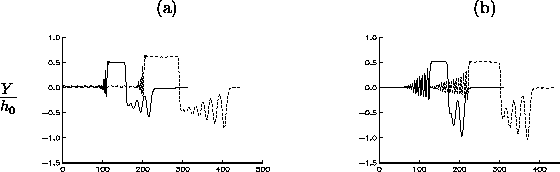
In the next example we consider the same problem as above, but let the body have speed U/c₀=1.09. Now we also want to vary the thickness of the body, to investigate the effect of various forcing. In the first case (figure 3a) the thickness of the body is H₀=0.4h₂. Now the moving body generates a train of solitary waves propagating upstream, with an amplitude a=1.171h₂. We have compared the saturated leading waves with fully nonlinear solitary wave solutions of the corresponding steady problem, with a very high agreement (see also figure 4d for another example).

We then halve the thickness of the body ( H₀=0.2h₂) and display results in figure 3b. The generated solitary waves have now somewhat reduced amplitude and generation rate as compared to the previous example. The reduction of the body thickness is once more repeated (figure 3c), i.e. H₀=0.1h₂, but still upstream solitary waves are generated, now with a quite reduced generation rate, however. When the height of the body is reduced still more, to H₀=0.05h₂, solitary waves are not generated. The flow becomes supercritical, with a minor depression moving with the same speed as the body (figure 3d).

In another example the two-fluid system at rest has thicknesses h₁ and h₂=4h₁ (a thin layer below a thick) and ratio between the densities $\rho _2/\rho _1=0.7873$. A half-elliptical body with horizontal and vertical half-axes 10h₁and 0.1h₁, respectively, is moving horizontally with speed U=1.1c₀ along the bottom of the lower (thinner) layer. This geometry has approximately the same volume as the former one but is more slender, and therefore imposes weaker nonlinearity on the problem. Still upstream solitary waves with height of the order of the thinner layer are generated, see figure 4.

For both geometries we have found that solitary waves are generated for a rather narrow interval of the speed, i.e. 1.05<U/c₀<1.15, approximately. The generated solitary waves have always an amplitude comparable to the depth of the thinner layer.
 

Topography in the thicker layer

We have also performed some simulations for a body moving horizontally with constant speed in the thicker of the two layers (results not shown). If the lower layer is the thicker one, a depression of the interface develops behind the body. This depression may be rather significant, depending on the size of the body. Correspondingly, the interface is lifted upstream of the body. We have not observed that waves are generated upstream for this configuration.

Another interesting problem, which we have not yet investigated, is that with an oscillatory flow at stationary body, which is relevant to tidal driven flow at a bottom topography. We aim to perform simulations for this problem and present the results at the workshop.
 

Comparison with experiments

In the ocean (or in the atmosphere) the density profile is seldom very sharp, and one may question the relevance of a two-layer model where two homogeneous fluids are separeted by a sharp interface. On the otherhand, if an infinitely sharp pycnocline could be created in nature, one would expect any wave motion to break up due to the Kelvin-Helmholtz instability. In order to investigate these issues we have performed several experiments in a wave tank on internal solitary waves. The solitary waves may propagate along a pycnocline separating a thinner layer of fresh water above a thicker layer of brine. The thickness of the pycnocline is in the interval 0.13 - 0.26 times the depth of the thinner layer, approximately. The induced fluid velocities are measured quite accurately using Particle Tracking Velocimetry. In figure 2 we show an example of the velocity profile at the crest of a solitary wave. Data from several experiments are included. Also is shown a comparison with the fully nonlinear theory, with good agreement. We have performed several other experiments, also with good agreement with theory (results may be found in reference 2). We have observed that Kelvin-Helmholtz instability only occurs for the largest waves (close to the maximal amplitude). Instability appears to occur according to the theorem of Miles and Howard.

This research was supported by The Research Council of Norway.
 

References

GRUE, J., FRIIS, H. A., PALM, E. AND RUSåS, P. O. A method for computing unsteady fully nonlinear interfacial waves. J. Fluid Mech., 351, 1997.

GRUE, J., JENSEN, A., RUSåS, P. O. AND SVEEN, J. K. Properties of large amplitude internal waves. J. Fluid Mech. (to appear). 1998.




 
 

Figure 1: Elevation of interface. (a) U/c₀=0.81. (b) U/c₀=0.94. t(g/h₂)^1/2=480 (solid line), t(g/h₂)^1/2=870 (dashed line). $\rho _2/\rho _1=0.8114$, h₁/h₂=4. (t=time.)

 

Figure 2: Velocity profile u(y)/c₀ at the crest of solitary wave. c₀ the linear shallow water speed. Depth of upper layer: h₂. Depth of lower layer: h₁=4.13h₂. Amplitude a=0.78h₂. $\rho _2/\rho _1=0.975$. Dots: Experiments. Solid line: Fully nonlinear theory.

 
 

 

Figure 3: Elevation of interface. Fr=1.09. Decreasing height H₀ of moving geometry, i.e. H₀sech²Kx. t(g/h₂)^1/2=1020 (dashed line) t(g/h₂)^1/2=1500 (solid line). Height of the body: a) H₀=0.4h₂. b) H₀=0.2h₂. c) H₀=0.1h₂. d) H₀=0.05h₂. $\rho _2/\rho _1=0.8114$, h₁/h₂=4. (Note the differences in vertical scale.)

Figure 4: Generation of upstream solitary waves. Moving bottom topography being a half ellipse, horizontal half-axis 10h₁, vertical half-axis 0.1h₁. U/c₀=1.1, $\rho _2/\rho _1=0.7873$, h₂/h₁=4. a) t(g/h₁)^1/2=1080. b) t(g/h₁)^1/2=1920. c) t(g/h₁)^1/2=2760. d) Close up of figure c), black squares mark steady solitary wave solution with |Y|_max/h₁=0.869.

 

1998-09-10