


Next: `Rigid-Lid' case
Up: On the maximal form
Previous: Introduction
The Conjugate flow equations
Consider flow in a 2-layer system, where in one region we have
uniform flow where the lower layer has velocity, c1, depth h1 and
density  and the upper layer has c2, h2 and
and the upper layer has c2, h2 and  .
For
our purposes here we have that c1=c2=c i.e. both outskirts layer
flow velocities are equal to (minus) the wave velocity. Suppose over
some ``surge-region'', this uniform flow transformed into a distinct
uniform flow where the corresponding velocities are now
.
For
our purposes here we have that c1=c2=c i.e. both outskirts layer
flow velocities are equal to (minus) the wave velocity. Suppose over
some ``surge-region'', this uniform flow transformed into a distinct
uniform flow where the corresponding velocities are now
 and
and
 and the depths
and the depths
 and
and
 .
For our
purposes here Benjamin (1966) defined such regions of uniform 2-layer
flows as being ``conjugate'' to each other if
.
For our
purposes here Benjamin (1966) defined such regions of uniform 2-layer
flows as being ``conjugate'' to each other if
- 1.
- the fluid flux in every layer is equal in both regions i.e.
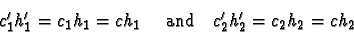 |
(1) |
- 2.
- the momentum flux in both regions are equal i.e.
where pt and
 are the pressures at the top surfaces of the
upper layers in both uniform flow regions respectively.
are the pressures at the top surfaces of the
upper layers in both uniform flow regions respectively.
- 3.
- the energy flux in both regions are equal or, equivalently, we
can obtain a relation by summing all the pressure changes round a large
loop bounded by the upper and lower streamlines and with vertical
``arms'' in the regions of uniform flow. This latter form is more
convenient when we consider ``free top-surface'' boundary conditions.
In the rigid lid flat-topped case we have, from Bernoulli's
equation
 |
(3) |
or, alternatively, for the free surface case,
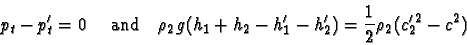 |
(4) |
Applying Bernoulli's equation along the bottom streamline gives the
difference between the bottom pressures, pb and
 viz.
viz.
In either case, as the sum of the pressure changes round the closed
path must add to zero,
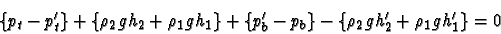 |
(5) |
With h1, h2 given, the above effectively constitute seven
equations in seven unknowns,
 ,
,
 ,
c,
,
c,
 ,
,
 ,
,
 and
and
 .
However they are easily reducible to virtually two equations in two
unknowns, that can be taken as c2/gh2 and
.
However they are easily reducible to virtually two equations in two
unknowns, that can be taken as c2/gh2 and
 ,
that can
then be easily solved by the Newton method.
,
that can
then be easily solved by the Newton method.



Next: `Rigid-Lid' case
Up: On the maximal form
Previous: Introduction
1998-09-18
![]() and the upper layer has c2, h2 and
and the upper layer has c2, h2 and ![]() .
For
our purposes here we have that c1=c2=c i.e. both outskirts layer
flow velocities are equal to (minus) the wave velocity. Suppose over
some ``surge-region'', this uniform flow transformed into a distinct
uniform flow where the corresponding velocities are now
.
For
our purposes here we have that c1=c2=c i.e. both outskirts layer
flow velocities are equal to (minus) the wave velocity. Suppose over
some ``surge-region'', this uniform flow transformed into a distinct
uniform flow where the corresponding velocities are now
![]() and
and
![]() and the depths
and the depths
![]() and
and
![]() .
For our
purposes here Benjamin (1966) defined such regions of uniform 2-layer
flows as being ``conjugate'' to each other if
.
For our
purposes here Benjamin (1966) defined such regions of uniform 2-layer
flows as being ``conjugate'' to each other if
![]() ,
,
![]() ,
c,
,
c,
![]() ,
,
![]() ,
,
![]() and
and
![]() .
However they are easily reducible to virtually two equations in two
unknowns, that can be taken as c2/gh2 and
.
However they are easily reducible to virtually two equations in two
unknowns, that can be taken as c2/gh2 and
![]() ,
that can
then be easily solved by the Newton method.
,
that can
then be easily solved by the Newton method.