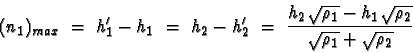`Rigid-Lid' case

In this case, the conjugate flow equations, can be algebraically solved as was done by Amick and Turner (1986) who gave the limiting amplitude as

$$(n_1)_\mathit{max} \ =\ h_1^\prime - h_1 \ =\ h_2 - h_2^\prim... ...qrt{\rho_1} - h_1\sqrt{\rho_2}}{\sqrt{\rho_1} + \sqrt{\rho_2}}$$ (6)

and the limiting wave's velocity as

$$c = \left.\left[g\left(h_1+h_2\right) \left(1-\frac{\rho_2}... ...1}{2}}\right/ \left[1+\sqrt{\frac{\rho_2}{\rho_1}}\;\,\right]$$ (7)

Note, in particular, that Amick and Turner's equation, (6), implies positive/negative waves if $(h_2/h_1)^2 \gtrless \rho_2/\rho_1$, as has also been subsequently concluded by several others e.g. Craig and Sternberg (1991).

For the case, h₂/h₁=1/3 and $\rho _2/\rho _1=0.997$, we see from Fig. 2 that the largest computed amplitude is $\sim -0.99\,h_2$, and, indeed, the velocity of the largest computed wave is also $\sim 0.0548\sqrt{gh_2\,}$. These values agree precisely with the predicted conjugate flow amplitude of $h_1^\prime - h_1= -0.99849775\,h_2$ and velocity of $c= 0.05481339\sqrt{gh_2\,}$, as evaluated from (6) and (7). Further the trough becomes increasingly flatter in line with what would be expected if a uniform mid-section flow were to develop. There can be no doubt that the limit of the numerical solution branch investigated by Evans and Ford (1996b) is explicable in terms of conjugate flow in precisely the way Turner and Vandenbroeck (1988) advocated.

This conclusion is of some interest for large amplitude overhanging (or underhanging) profiles have been numerically found by Meiron and Saffman (1983) and Grimshaw and Pullin (1986). However, these calculations were of periodic internal waves, and it would appear that they became overhanging only because the imposed periodicity prevented their widths from expanding beyond the periodic length. At least along the solution branch investigated, solitary internal 2-layer waves never develop an infinitely steep gradient and, accordingly, never become overhanging.